A Shooting Model – An Exp(G)lanation and Application

If you’re a follower of the growing analytics movement in football you’ll probably have heard of the term ‘expected goals model’. The term may have been shortened to ExpG, xG or something, but whatever it’s been named, it’s basically a shots model.

What’s a shots model, then?

A shots model puts a theoretical goal value on a shot that a team or player takes during a game.

The value of a shot is either 0 (no goal) or 1 (a goal) isn’t it? So what’s the point?

Yep, the final outcome is always 0 or 1. However, in order to better analyse teams (and players) it’s not really good enough to say x scored 55 goals this season and y scored 60. It still begs the question of why that was the case. Did x have less shots? Did y have easier chances?

Ok, you can count up shots, but how do you quantify how easy a chance is?

We can begin to assign an ‘expected goal’ value for each shot by looking back into history. Not all shots are the same, so you have to group similar ones together. How often over time is the same type of chance converted? Working this out will give us an ‘expected goal’ value. Personally, I’m not sure I like the term ‘expected’ goal – it’s more of an average benchmark score to simply compare each team or player’s shots. However, expected goals is how it’s mostly referred to so I’ll stick with.

Surely there are too many variables to just lump shots together like this?

Each expected goals model that you come across will have different inputs. All of them use the location of where the shot was taken from. However, each model will be different in how detailed its location data is. Some models will take into account how the ball was delivered to the person making the shot (through ball, cross etc), and some will take into account whether the shot was made by foot or by header. Some models take into account all shots (on target, off target, blocked) and some take into account ball placement (in the corner, straight down the middle). What’s missing from all models in the public domain is defensive positioning – where are defenders in relation to the shooter? However, some modellers talk of adding ‘game state’ into the mix as a proxy for this – conversion rates vary depending on the scoreline (the theory being teams change the balance of their attack/defence based on what the score is).

So what does your model use?

My current model uses only shots on target. The only other driver is where on the pitch the shot was taken from. I split shots into 46 ‘bins’. Direct free kicks and penalties have their own bins:

Is that it? How much data have you got?

Yep, that’s it – I want to keep the model as simple as possible to understand while still having something that works. I have over 13000 shots on target recorded covering the last four Premier League seasons.

How do you apply the data?

As I’ve said, those 13000-odd shots have been put into the 46 location bins plus the direct free kick and penalty ones. That gives me an average goal value for each of those shot location bins. For example, a shot on target from bin 14 is worth a theoretical 0.59 goals. If a team gets a shot on target from bin 5 it’s worth a theoretical 0.91 goals. I can then tot up a team or players shots over a season to find out what the average team/player benchmark would be for those shots.

Using a mathematical technique called linear regression, I can see how well the model fits to each of the 80 team performances over the last 4 seasons. I can plot the theoretical (or expected) goal difference for each team against the actual goal difference they recorded that season. In other words, what’s the correlation between shot on target location (for and against) and goal difference? A perfect correlation would return a ‘r2’ value of 1. If there was no relationship it would return a ‘r2’ value of 0. As it turns out the r2 value returned is a healthy 0.878:

I’m still not sure where this is going?

Prozone’s Omar Chaudhuri has shown on his blog 5addedminutes why goal difference is a good indicator of the sustainability of a team’s long term results and why sometimes, the league table does lie.

If the relationship between Expected Goal Difference (ExpGD) and Actual Goal Difference is strong, and the relationship between Actual Goal Difference and Actual Points is strong, then it follows that ExpGD matters when it comes to placings and points in the league table.

Man United’s ExpGD was in the 20s in the first three years of this model. This year it was less than 12. Man City’s ExpGD in the first year of this model was barely over 2. It ballooned into the 30’s and 40’s the last three years and they’ve won the league twice in that time.

Liverpool’s ExpGD started in the late teens in the first year and it’s risen every year since and into the 30’s this season. Arsenal are the opposite of Liverpool and is posting ever decreasing ExpGDs. Arsenal keep having to battle right to the end to ensure Champions League football whereas previously it was almost a given. These baseline numbers matter – they are a great explanation of what actually happens over time.

If we looked at these team’s possession figures, it wouldn’t tell us anywhere near the same story. I tested the correlation of all teams’ possession% with its goal difference during the same period in the Premier League. The r2 value was a much lower 0.546.

Is the model any good at predicting what’s going to happen the following season?

If I plot a team’s ExpGD one year against the one it’s posted the following year, this is what it looks like:

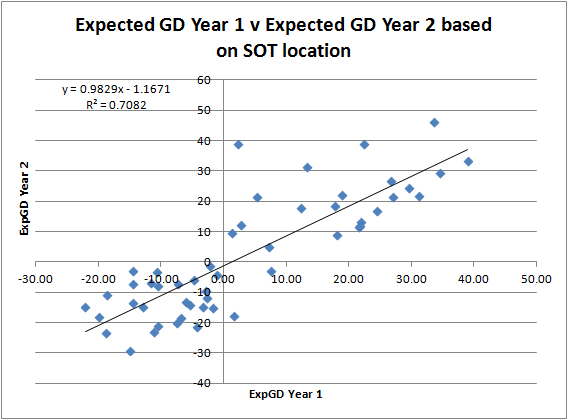Again the relationship looks decent with an r2 of 0.7082. However, there’s some whopping outliers – Man City’s hugely positive change from 2010/11 to 2011/12 being the main one.

How about predicting what’s actually going to happen the following year?

Ok, I can also plot ExpGD one year to ActualGD the next and it looks like this:

Again that Man City improvement in 2011/12 alone make the figures look worse than the overall trend might actually be. I expect to be able to show a better predictive value of ExpGD as more data is added to the model as seasons go by.

As the model currently stands, this is how it would predict the league table to look next season if I firstly just used last season’s numbers to predict it (left) or forecast it using 2011-14 numbers to predict it (right):

For the purposes of the newly promoted teams I just used the average of previously promoted teams ExpGDs. I also used the formula in that Omar Chaudhuri piece I mentioned up top, to simply convert GD to points.

Got any comments, questions or criticisms? I’m sure you have. My aim is to try and make the analytics movement as open as possible. I’m still learning myself every day and continually try to make things as understandable as possible. Inevitably things still turn out too mathy, but it comes with the territory.

Get in touch on Twitter @footballfactman or comment below.

 

 

 

Advertisement